I
-
I
-
Resolving
Small
Signals
Hidden
by
Large
Signals
Using
the
Resolution
Bandwidth
Function
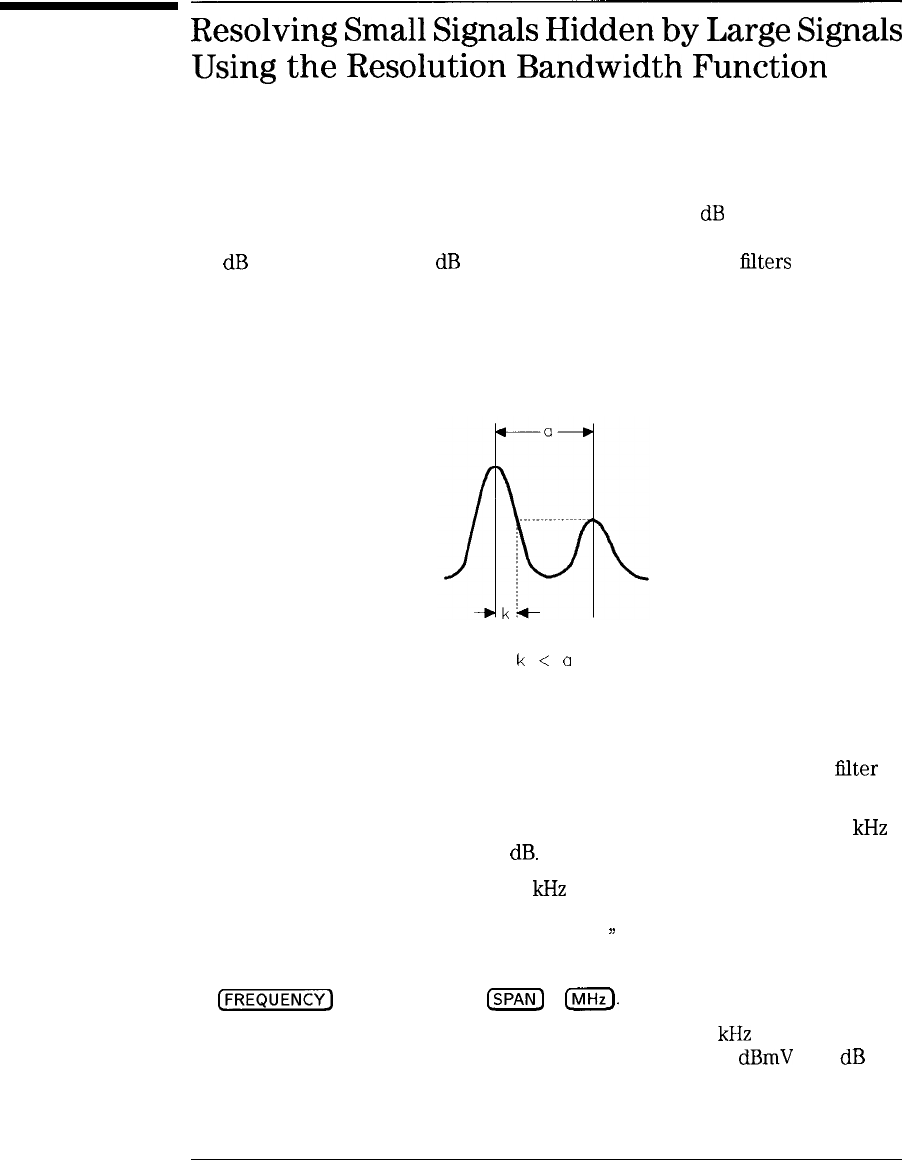
When dealing with resolution of signals that are not equal in amplitude, you
must consider the shape of the IF filter as well as its 3
dB
bandwidth. The
shape of the filter is defined by the shape factor, which is the ratio of the
60
dB
bandwidth to the 3
dB
bandwidth. (Generally, the IF lilters in this
spectrum analyzer have shape factors of 15: 1 or less.) If a small signal is
too close to a larger signal, the smaller signal can be hidden by the skirt of
the larger signal. To view the smaller signal, you must select a resolution
bandwidth such that k is less than a. See Figure 4-3.
k
<
a
Figure 4-3. Resolution Bandwidth Requirements for Resolving Small Signals
The separation between the two signals must be greater than half the filter
width of the larger signal at the amplitude level of the smaller signal.
Example: Resolve two input signals with a frequency separation of 200
kHz
and an amplitude separation of 60
dB.
1. To obtain two signals with a 200
kHz
separation, connect the equipment
as shown in the previous section,
“Resolving Signals of Equal Amplitude
Using the Resolution Bandwidth Function.
))
2. Set the center frequency to 300 MHz and the span to 2 MHz: press
FREQUENCY)
300 (MHz), then
ISPAN]
2
@.
3. Set the source to 300.2 MHz, so that the signal is 200
kHz
higher than the
calibration signal. Set the amplitude of the signal to -31
dBmV
(60
dB
below the calibration signal).
4-6
